液体の持つエネルギー
液体の持つエネルギーは位置エネルギー、圧力エネルギー、速度エネルギーの3つです。
ベルヌーイの定理はこの3要素で構成されているため、それぞれをまず解説します。
位置エネルギー
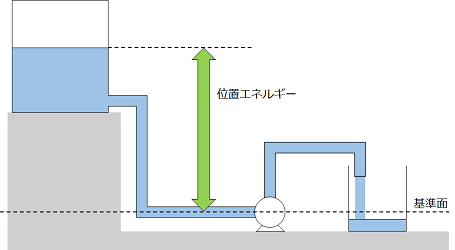
ある基準面よりも高い位置にある液は位置エネルギーを持ちます。
位置エネルギー[J/kg]$$gz$$g:重力加速度[m/s2]、z:高さ[m]
また基準面より低い位置にある液はマイナスの位置エネルギーを持ちます。
これは基準面をどこに設けるかによるだけで、意味は変わりません。
この位置エネルギーに逆らって上に液体を移送するのがポンプです。
圧力エネルギー
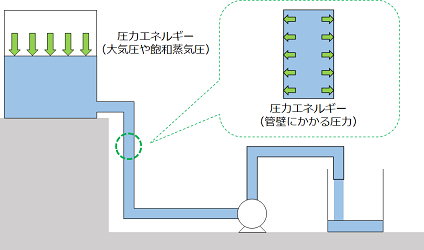
タンクの液面には大気圧や飽和蒸気圧などの圧力がかかります。
これら液面にかかる圧力が圧力エネルギーです。
圧力エネルギー[J/kg]$$\frac{P}{\rho}$$P:圧力[Pa]、ρ:密度[kg/m3]
また配管内においては管壁にかかる圧を圧力エネルギーと考えます。
配管内への圧力は上位にあるタンクからの圧力(ヘッド圧)はもちろん、ポンプの送液圧力によってもかかります。
速度エネルギー
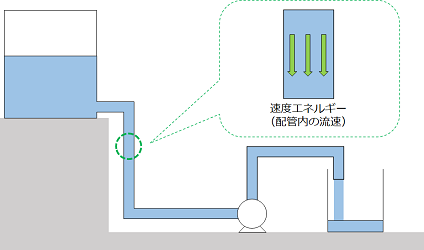
配管内を流れる流体は速度エネルギーを持ちます。
配管内の流速によって速度エネルギーは決定します。
速度エネルギー[J/kg]$$\frac{ \ u^2 \ }{2}$$u:速度[m/s]
配管流速は連続の式を利用して配管断面積[m2]や体積流量[m3/s]から算出可能です。
質量流量[kg/s]を測定している場合は測定箇所の密度[kg/m3]も必要となります。
ベルヌーイの定理
ベルヌーイの定理は、これまで紹介した位置エネルギーや圧力エネルギー、速度エネルギーの和が一定になることを示したものです。
この式は理想流体において成立します。
つまり摩擦や渦によるエネルギーの損失が無いものとして考えます。
エネルギーでの表現
ベルヌーイの定理は以下のように表します。
ベルヌーイの定理[J/kg]$$gz+\frac{P}{\rho}+\frac{ \ u^2 \ }{2}=一定$$ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
圧力での表現
ベルヌーイの定理に密度ρをかけることで圧力換算でも表現可能です。
このときの圧力エネルギー部分(P)を静圧、速度エネルギー部分(ρu2/2)を動圧、そして静圧と動圧の和を全圧と呼びます。
ベルヌーイの定理(圧力換算)[Pa]$$\rho gz+P+\frac{ \rho \ u^2\ }{2}=一定$$ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
水頭(ヘッド)での表現
エネルギーの大きさを基準面からの高さに換算したものを水頭(ヘッド)と呼びます。
変換後の値は速度水頭、位置水頭、圧力水頭と呼ばれます。
重力加速度gで割ることで算出されます。
ベルヌーイの定理(水頭換算)[m]$$z+\frac{P}{\rho g}+\frac{ \ u^2 \ }{2g}=一定$$ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
圧力損失の考慮
ベルヌーイの定理は理想流体であること、つまり非粘性である場合に成り立ちます。
ただし実際は流体の粘性により管内摩擦が発生したり、配管継手部分にて渦によるエネルギー損失が発生したりします。
これら損失を圧力損失と呼びます。
ベルヌーイの定理に圧力損失、さらにポンプやブロワなどから加える動力を補正項として加えることで実用的な計算が可能になります。
この式を機械的エネルギー収支式と呼びます。
機械的エネルギー収支式[J/kg]$$gz_1+\frac{P_1}{\rho}+\frac{ \ u_1^2 \ }{2}+W=gz_2+\frac{P_2}{\rho}+\frac{ \ u_2^2 \ }{2}+F$$ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]、W:外部動力[J/kg]、F:圧力損失[J/kg]
圧力損失Fはファニングの式より求めることができます。
オススメ書籍
・明解入門 流体力学(第2版)
少し慣れてきて、流体の勉強を頑張りたいときにオススメです。
ページ数が少ないものの丁寧に解説されています。
-

-
明解入門 流体力学(第2版)
www.amazon.co.jp
・化学工学ー解説と演習ー
化学工学を勉強したい!と思ったら真っ先にオススメしたい書籍です。
他の汎用化学工学書籍には無い「撹拌動力計算」や「撹拌伝熱計算」も記載されています。
-

-
化学工学―解説と演習ー
www.amazon.co.jp
・化学プラント配管設計の基本
伝熱の種類、熱伝導の計算、熱交換器の種類について記載されています。
その他、化学工学の基本事項が解説された後、それらを踏まえて化学プラントにおける配管設計の基礎から詳細に解説される書籍です。
この1冊で配管設計を一通り勉強できます。
-

-
化学プラント配管設計の基本―配管技術者への道しるべ
www.amazon.co.jp




