トリチェリの定理はベルヌーイの定理から導かれる代表的な近似式です。
タンク出口から液が排出されてもタンク液面高さが極微小しか変化しない時、トリチェリの定理が適用できます。
ベルヌーイの定理から導出しているため、圧力損失等は無いものとして考えられた式です。
トリチェリの定理
$$u_2=\sqrt {2gz}$$
g:重力加速度[m/s2]、z:液面高さ[m]、u2:排出口流速[m/s]
ベルヌーイの定理を確認
ベルヌーイの定理は位置エネルギー、圧力エネルギー、速度エネルギーの和が一定になることを示したものです。
この式を基本にトリチェリの定理は考えられます。
ベルヌーイの定理[J/kg]
$$gz+\frac{P}{\rho}+\frac{ \ u^2 \ }{2}=一定$$
ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
トリチェリの定理を導出
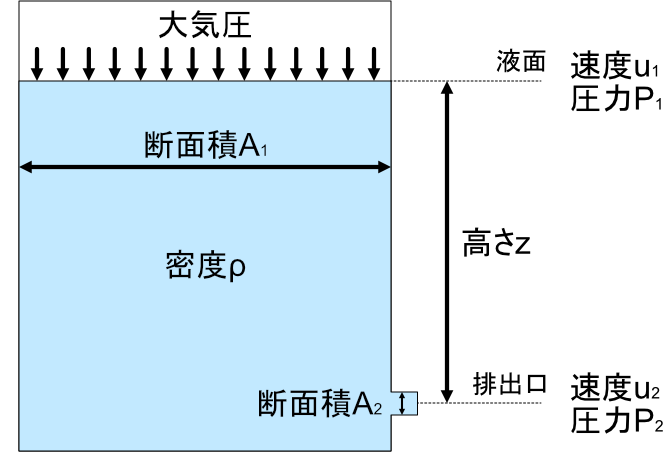
タンクの底部側面から液が排出される場合を考えます。
液面は排出口からz[m]の高さにあり、液体の密度はρ[kg/m3]とします。

ベルヌーイの定理を適用
タンク液面と排出口におけるベルヌーイの定理式は以下のように表現できます。
①液面、②排出口におけるベルヌーイの定理式
$$gz+\frac{P_1}{\rho}+\frac{ \ u_1^2 \ }{2}=\frac{P_2}{\rho}+\frac{ \ u_2^2 \ }{2}$$
ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
圧力は等しい
タンク液面と排出口は共に大気に接しています。
そのため両位置にかかる圧力はどちらも大気圧です。
圧力を共通のPに変更
$$gz+\frac{P}{\rho}+\frac{ \ u_1^2 \ }{2}=\frac{P}{\rho}+\frac{ \ u_2^2 \ }{2}$$
ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
これにより圧力エネルギーに関する項(P/ρ)を削除できます。
圧力エネルギーの項を削除
$$gz+\frac{ \ u_1^2 \ }{2}=+\frac{ \ u_2^2 \ }{2}$$
g:重力加速度[m/s2]、z:高さ[m]、u:速度[m/s]
断面積を比較する(連続の式)
ここで連続の式について考えます。
連続の式は流体における質量保存則です。
密度を一定と考えれば配管断面積と流速が反比例します。
連続の式$$A_1 u_1=A_2 u_2$$A:断面積[m2]u:速度[m/s]
タンク液面と排出口の断面積を比較してタンク液面側の方が圧倒的に断面積が大きいと考えます。
その時、タンク液面側の流速はゼロとみなすことができます。
今回の場合はu1が該当します。
液面側の流速をゼロに近似
$$gz=\frac{ \ u_2^2 \ }{2}$$
g:重力加速度[m/s2]、z:高さ[m]、u:速度[m/s]
最後に出口流速を求める
タンク液面側の流速をゼロに近似したことで分かりやすい式に変化しました。
最後に式変形して排出口における流速を求めます。
これがトリチェリの定理です。
トリチェリの定理$$u_2=\sqrt {2gz}$$
g:重力加速度[m/s2]、z:高さ[m]、u:速度[m/s]
まとめ
トリチェリの定理はベルヌーイの定理から導かれる代表的な近似式です。
ベルヌーイの定理[J/kg]
$$gz+\frac{P}{\rho}+\frac{ \ u^2 \ }{2}=一定$$
ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
以下の条件が満たせる場合、トリチェリの定理が利用できます。
- タンク液面と排出口は共に圧力が同じ(例:どちらも大気圧がかかっている)
- タンク液面と排出口の断面積を比較してタンク液面側の方が圧倒的に断面積が大きい
- 圧力損失が無い
ベルヌーイの定理[J/kg]
$$gz+\frac{P}{\rho}+\frac{ \ u^2 \ }{2}=一定$$
ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
オススメ書籍
・明解入門 流体力学(第2版)
少し慣れてきて、流体の勉強を頑張りたいときにオススメです。
ページ数が少ないものの丁寧に解説されています。
-

-
明解入門 流体力学(第2版)
www.amazon.co.jp
・化学工学ー解説と演習ー
化学工学を勉強したい!と思ったら真っ先にオススメしたい書籍です。
他の汎用化学工学書籍には無い「撹拌動力計算」や「撹拌伝熱計算」も記載されています。
-

-
化学工学―解説と演習ー
www.amazon.co.jp
・化学プラント配管設計の基本
伝熱の種類、熱伝導の計算、熱交換器の種類について記載されています。
その他、化学工学の基本事項が解説された後、それらを踏まえて化学プラントにおける配管設計の基礎から詳細に解説される書籍です。
この1冊で配管設計を一通り勉強できます。
-

-
化学プラント配管設計の基本―配管技術者への道しるべ
www.amazon.co.jp


