撹拌所要動力は動力数Npという無次元数の形で算出します。
撹拌条件や液性状から動力に換算します。
動力数
$$ N_{ p } = \frac{ P }{ \rho n^3 d^5 }=Re\frac{ P }{ \mu n^2 d^3 }$$Np:動力数[-]、P:動力[W]、ρ:密度[kg/m3]
n:回転数[1/s]、d:翼径[m]、μ:粘度[Pa・s]、Re:撹拌レイノルズ数[-]
動力数は条件によって様々な算出方法があります。
- 撹拌翼の種類(パドル、アンカー等)
- レイノルズ数(層流や乱流)
- 邪魔板の有無
- 邪魔板の取り付け条件(完全邪魔板条件かどうか)
上記の条件から該当する計算式を活用してください。
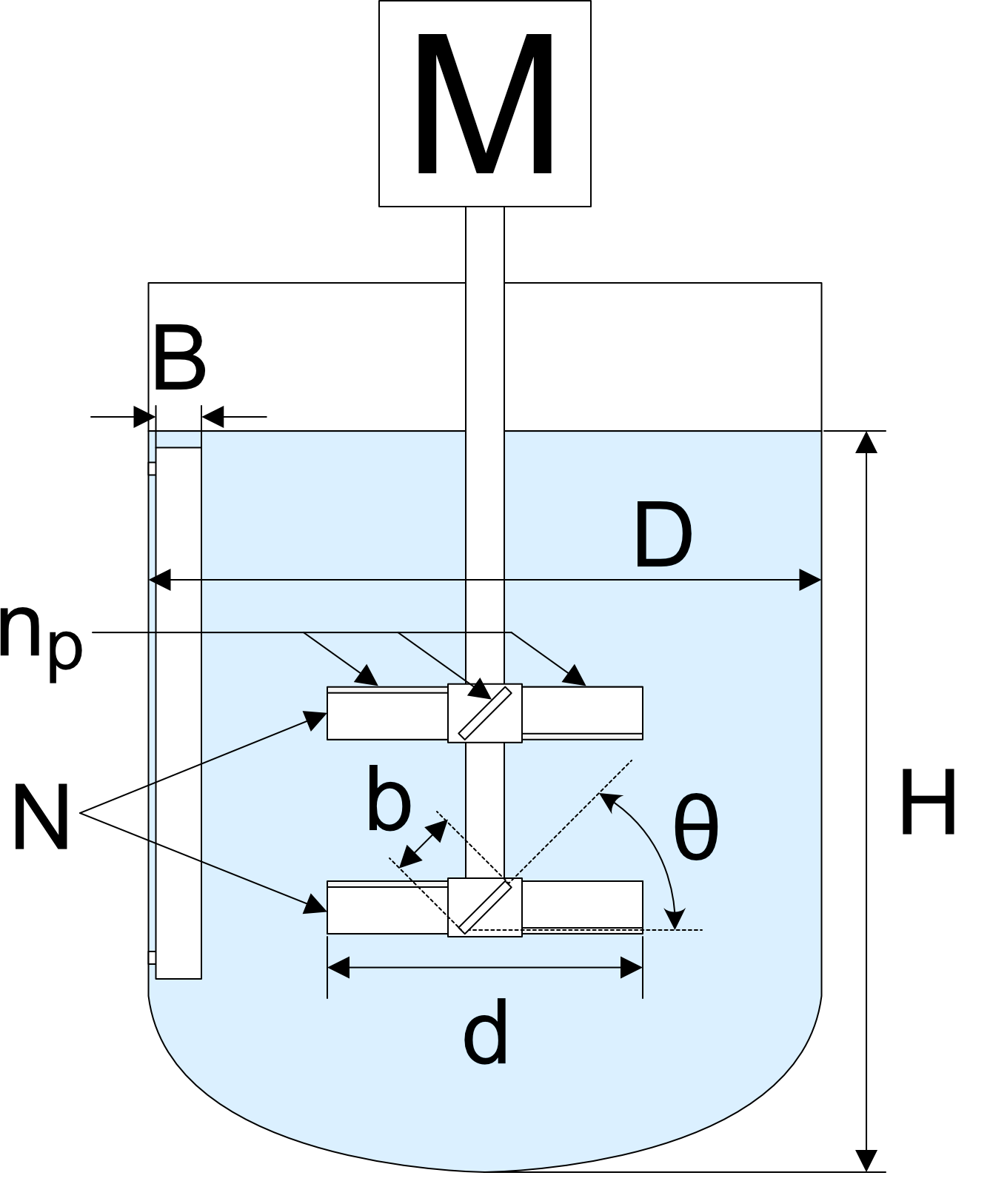
各パラメータの対応箇所
H:液深さ[m]、D:槽径[m]、b:翼幅[m]、d:翼径[m]、θ:羽根取り付け角度[deg]は以下の値を指します。
またnp:羽根枚数[-]は一つの撹拌翼についた羽根の枚数を、N:翼段数[-]はシャフトに取りつけられた撹拌翼の個数を表します。
撹拌動力の基本知識
動力推算の前に、撹拌特有の動力に関する要素を解説します。
撹拌所要動力の定義
撹拌エネルギーはモーターのトルクを軸(シャフト)経由で撹拌翼に与えます。
撹拌所要動力は以下の式が基本です。
撹拌所要動力
$$ P=2\pi nT$$P:撹拌所要動力[kW]、n:回転数[1/s]、T:トルク[N・m]
ラボ実験などでは回転計とトルク計で計測して撹拌所要動力を評価します。
撹拌所要動力をタンク内の流体量で割ることで、単位体積当たりの動力として評価します。
単位体積あたりの撹拌所要動力
$$ P_{V}=\frac{P}{V}$$Pv:単位体積あたりの撹拌所要動力[kW/m3]
P:撹拌所要動力[kW]、V:液量[m3]
動力数としての表現
撹拌所要動力は動力数という無次元数で整理されます。
動力数
$$ N_{ p } = \frac{ P }{ \rho n^3 d^5 }=Re\frac{ P }{ \mu n^2 d^3 }$$Np:動力数[-]、P:動力[W]、ρ:密度[kg/m3]
n:回転数[1/s]、d:翼径[m]、μ:粘度[Pa・s]、Re:撹拌レイノルズ数[-]
動力数と撹拌レイノルズ数の関係をNp-Re曲線で表すことで撹拌装置としての性能を表現します。
撹拌装置の設計においては、動力数を求めて撹拌所要動力を想定します。
邪魔板なし条件での動力推算
まず構造的に簡易である邪魔板(バッフル)なしでの動力推算を解説します。
高レイノルズ数領域において、基本的に邪魔板なし条件では、レイノルズ数の増加とともに動力数が減少する傾向にあります。
永田の式
パドル翼に関する代表的な推算式として永田の式があります。
永田の式は翼幅と液深さの比(b'/H)が1を超えない範囲で利用できます。
永田の式
$$ N_{P}=\frac{A}{Re}+B\left(\frac{10^{3}+1.2{Re}^{0.66}}{10^{3}+3.2{Re}^{0.66}}\right)^{p}\left(\frac{H}{D}\right)^{\left(0.35+b/D\right)}$$
$$ \begin{align}
A&=14+\frac{b}{D}\left\{670\left(\frac{d}{D}-0.6\right)^{2}+185\right\}\\\\
B&=10^\left\{{1.3-4(b/D-0.5)^{2}-1.14(d/D)}\right\}\\\\
p&=1.1+4\left(\frac{b}{D}\right)-2.5\left(\frac{d}{D}-0.5\right)^{2}-7\left(\frac{b}{D}\right)^4
\end{align}$$
NP:動力数[-]、Re:撹拌レイノルズ数[-]、H:液深さ[m]
D:槽径[m]、b:翼幅[m]、d:翼径[m]
永田の式は羽根枚数np=2での推算式であり、羽根枚数が違ったり多段翼で用いたりする場合は、厚みのある2枚羽根1段パドル翼に修正して用います。
パドル翼条件の修正
$$ b^{'}=\frac{n_{p}}{2}bN$$
b':修正した翼幅[m]、np:羽根枚数[-]、b:翼幅[m]、N:翼段数[-]
亀井・平岡の式
永田の式よりも複雑ですが、幅広いレイノルズ数・撹拌翼へ利用できる亀井・平岡の式があります。
この式はパドル翼に対して開発されましたが、そのままタービン翼やアンカー翼に対しても利用できます。
アンカー翼は非常に太く厚みのあるパドル翼と考えて翼径dや翼幅bを設定します。
亀井・平岡の式
(パドル翼、タービン翼、アンカー翼)
$$ N_{p0}=\frac{1.2\pi^{4}\beta^{2}}{8d^{3}/\left(D^{2}H\right)}f$$
$$ \begin{align}
f&=\frac{C_{L}}{Re_{G}}+C_{t}\left\{\left(\frac{C_{tr}}{Re_{G}}+Re_{G}\right)^{-1}+\left(\frac{f_{\sim}}{C_{t}}\right)^{1/m}\right\}^{m}\\\\
Re_{d}&=\frac{nd^{2}\rho}{\mu}\\\\
Re_{G}&=\frac{\pi\eta\ln\left(D/d\right)}{4d/\beta D}Re_{d}\\\\
C_{L}&=0.215\eta n_{p}\frac{d}{H}\left\{1-\left(\frac{d}{D}\right)^{2}\right\}+1.83\frac{b\sin\theta}{H}\left(\frac{n_{p}}{2\sin\theta}\right)^{1/3}\\\\
C_{t}&=\left\{\left(1.96X^{1.19}\right)^{-7.8}+\left(0.25\right)^{-7.8}\right\}^{-1/7.8}\\\\
m&=\left\{\left(0.71X^{0.373}\right)^{-7.8}+\left(0.333\right)^{-7.8}\right\}^{-1/7.8}\\\\
C_{tr}&=23.8\left(\frac{d}{D}\right)^{-3.24}\left(\frac{b\sin\theta}{D}\right)^{-1.18}X^{-0.74}\\\\
f_{\sim}&=0.0151\left(\frac{d}{D}\right)C^{0.308}_{t}\\\\
X&=\gamma {n_{p}}^{0.7}b\left(\frac{\sin^{1.6}\theta}{H}\right)\\\\
\beta&=\frac{2\ln\left(D/d\right)}{\left(D/d\right)-\left(d/D\right)}\\\\
\gamma&=\left\{\frac{\eta\ln\left(D/d\right)}{\left(\beta D/d^{5}\right)}\right\}^{1/3}\\\\
\eta&=0.711\frac{0.157+n_{p}\ln\left(D/d\right)^{0.611}}{{n_{p}}^{0.52}\left[1-\left(d/D\right)^{2}\right]}
\end{align}$$
NP0:邪魔板なしの場合の動力数[-]、d:翼径[m]、D:槽径[m]
H:液深さ[m]、ρ:密度[kg/m3]、μ:粘度[Pa・s]
n:回転数[1/s]、np:羽根枚数[-]、θ:羽根取り付け角度[deg]、b:翼幅[m]
亀井・平岡の式は変数の値を変更することで様々な条件に対して利用できます。
撹拌翼ごとにパラメータを調整するため種類が多く、以下の記事でまとめています。
層流域における動力推算
2次元数値解析によって導き出された層流域における推算式です。
パドル翼はz=1, sinα=1, h=bとして計算します。
層流域における動力推算式
$$ N_{p}Re=8n_{p}+\frac{75.9z\left(n_{p}/{\sin\alpha}\right)^{0.85}\left(h/d\right)}{0.157+\left\{\left(n_{p}/\sin\alpha\right)\ln\left(D/d\right)\right\}^{0.611}}$$
NP:動力数[-]、Re:撹拌レイノルズ数[-]、np:羽根枚数[-]
h:翼高さ[m]、d:翼径[m]、D:槽径[m]
※パドル翼はz=1, sinα=1, h=b
zおよびsinαの値を変更することでアンカー翼やヘリカルリボン翼へ利用できます。
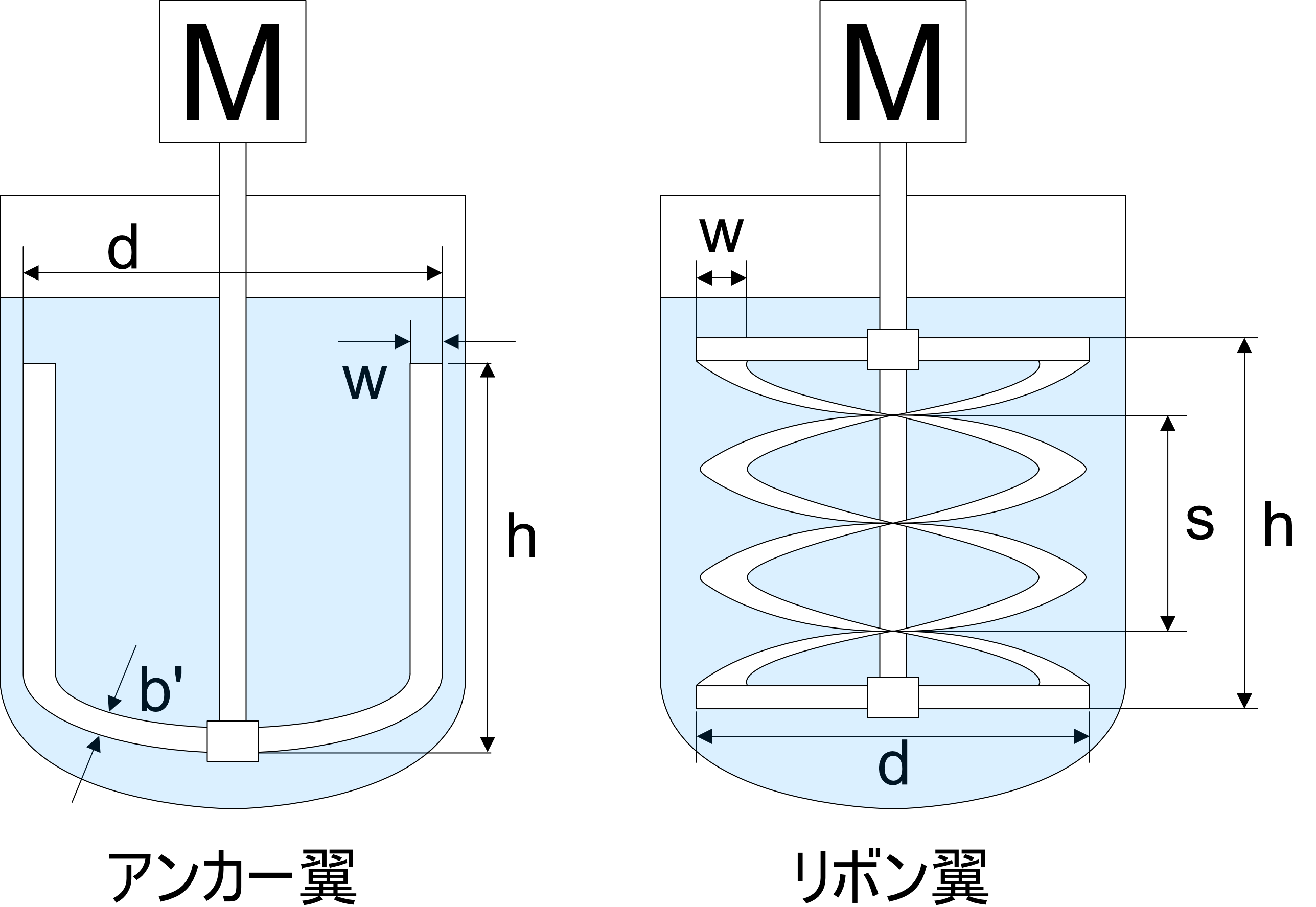
層流域における動力推算式(アンカー翼の変数)
$$ z=\frac{b^{'}}{h}+0.684\left\{n_{p}\ln\left(\frac{d}{d-2w}\right)\right\}^{0.139}$$
$$ \sin\alpha=1$$
b':腕部の翼幅[m]、h:翼高さ[m]、np:羽根枚数[-]
d:翼径[m]、w:翼幅[m]
層流域における動力推算式(ヘリカルリボン翼の変数)
$$ z=0.759\left\{\frac{n_{p}}{\sin\alpha}\ln\left(\frac{d}{d-2w}\right)\right\}^{0.139}\left\{n_{p}\ln\left(\frac{D}{d}\right)\right\}^{0.182}{n_{p}}^{0.17}$$
$$ \sin\alpha=\left\{1+\left(\frac{\pi d}{s}\right)^{2}\right\}^{-0.5}$$
np:羽根枚数[-]、d:翼径[m]、w:翼幅[m]
D:槽径[m]、s:翼ピッチ[m]
参考資料:2次元数値解析に基づく層流域の撹拌所要動力相関式の誘導(化学工学論文集 1994 年 20 巻 5 号 p. 595-603)
完全邪魔板条件での動力推算
高レイノルズ数域において、バッフルの枚数や幅を適切に選ぶことで最大の撹拌所要動力を得られます。
この時の条件を完全邪魔板条件と呼びます。
高レイノルズ数領域において、基本的に邪魔板あり条件では、レイノルズ数に関係なく動力数が一定の値を示す傾向にあります。
タンク形状からの推算
タンク形状からは以下の式で推算できます。
完全邪魔板条件での動力推算式(タンク形状より:パドル翼)
$$ \left(\frac{B}{D}\right){n_{B}}^{0.8}=0.27{N_{Pmax}}^{0.2}$$
B:邪魔板の幅[m]、D:槽径[m]、nB:邪魔板の枚数[-]
NPmax:完全邪魔板条件での動力数[-]
完全邪魔板条件での動力推算式(タンク形状より:傾斜パドル翼)
$$ \left(\frac{B}{D}\right){n_{B}}^{0.8}=0.44{N_{Pmax, \theta}}^{0.2}\left(\frac{2\theta}{\pi}\right)^{0.72}$$
B:邪魔板の幅[m]、D:槽径[m]、nB:邪魔板の枚数[-]
NPmax:完全邪魔板条件での動力数[-]
翼形状からの推算
翼形状からは以下の式で推算できます。
完全邪魔板条件での動力推算式(翼形状より:パドル翼)
$$ N_{Pmax}=\begin{cases}10\left({n_{p}}^{0.7}b/d\right)^{1.3} & {n_{p}}^{0.7}b/d\leq 0.54\\\\
8.3\left({n_{p}}^{0.7}b/d\right) & 0.54 < {n_{p}}^{0.7}b/d \leq 1.6\\\\
10\left({n_{p}}^{0.7}b/d\right)^{0.6} & 1.6 < {n_{p}}^{0.7}b/d\end{cases}$$
NPmax:完全邪魔板条件での動力数[-]
np:羽根枚数[-]、b:翼幅[m]、d:翼径[m]
完全邪魔板条件での動力推算式(翼形状より:傾斜パドル翼)
$$ N_{Pmax,\theta}=8.3\left(\frac{2\theta}{\pi}\right)^{0.9}\left(\frac{{n_{p}}^{0.3}b\sin^{1.6}\theta}{d}\right)$$
NPmax, θ:完全邪魔板条件での動力数[-]、np:羽根枚数[-]
b:翼幅[m]、d:翼径[m]、θ:羽根取り付け角度[rad]
スーパーミックスHR320のNPmaxは0.46、HR320Sは0.67を利用できます(動力数の参考資料)。
参考資料:傾斜パドル翼の撹拌所要動力の相関(化学工学論文集 1997 年 23 巻 6 号 p. 969-975)
任意の邪魔板条件での動力推算
完全邪魔板条件も含む、任意の邪魔板条件においては以下の動力推算式があります。
Npの計算値がNp0よりも小さかった場合は、Np0の値を採用します。
パドル翼(基本式)
基本式として、パドル翼における推算式が提案されています。
パドル翼に限らずxを変換することで様々な翼へ利用できます。
任意の邪魔板条件における動力推算式
$$ N_{p}=\left[\left(1+x^{-3}\right)^{-1/3}\right]N_{Pmax}$$
$$ x=4.5\left(\frac{B}{D}\right){n_{B}}^{0.8}\left(\frac{H/D}{{N_{Pmax}}^{0.2}}\right)+\frac{N_{P0}}{N_{Pmax}}$$
NP:動力数[-]、NPmax:完全邪魔板条件での動力数[-]、B:邪魔板の幅[m]
D:槽径[m]、H:液深さ[m]、NP0:邪魔板なしの場合の動力数[-]
傾斜パドル翼、プロペラ翼
傾斜パドル翼とプロペラ翼、3枚後退翼(ファウドラー翼)へはxを以下のように変更して利用します。
任意の邪魔板条件における動力推算式:変数変更部分
(傾斜パドル翼およびプロペラ翼)
$$ x=\frac{4.5\left(B/D\right){n_{B}}^{0.8}\left(h_{B}/H\right)}{{{\left(2\theta /\pi\right)}^{0.72}N_{Pmax}}^{0.2}}+\frac{N_{P0}}{N_{Pmax}}$$
NPmax:完全邪魔板条件での動力数[-]、B:邪魔板の幅[m]
D:槽径[m]、H:液深さ[m]、hB:邪魔板の長さ[m]
NP0:邪魔板なしの場合の動力数[-]
参考資料:傾斜パドル翼の撹拌所要動力の相関(化学工学論文集 1997 年 23 巻 6 号 p. 969-975)
マックスブレンド、フルゾーン、スーパーミックスMR205
メーカー各社が提供する大型オリジナル翼にも転用できます。
ここではマックスブレンド(住友重機械プロセス機器)、スーパーミックスMR205(佐竹マルチミクス)、フルゾーン(神鋼環境ソリューション)の式を紹介します。
任意の邪魔板条件における動力推算式:変数変更部分
(マックスブレンドおよびフルゾーン、スーパーミックスMR205)
$$ x=3.8\left(\frac{B}{D}\right){n_{B}}^{0.8}\left(\frac{H/D}{{N_{Pmax}}^{0.2}}\right)$$
NPmax:完全邪魔板条件での動力数[-]、B:邪魔板の幅[m]
D:槽径[m]、H:液深さ[m]、NP0:邪魔板なしの場合の動力数[-]
参考資料:大型翼の撹拌所要動力に対する液高さの影響(化学工学論文集 2016 年 42 巻 6 号 p. 187-191)
スーパーミックスHR320, HR320S
佐竹マルチミクスが提供するスーパーミックスHR320, HR320Sへはxを以下のように変更して利用します。
任意の邪魔板条件における動力推算式:変数変更部分
(スーパーミックスHR320およびHR320S)
$$ x=1.8\left(\frac{B}{D}\right){n_{B}}^{0.8}\left(\frac{H/D}{{\left(2\theta /\pi\right)}^{0.72}}\right)+\frac{N_{P0}}{N_{Pmax}}$$
NPmax:完全邪魔板条件での動力数[-]、B:邪魔板の幅[m]
D:槽径[m]、H:液深さ[m]、NP0:邪魔板なしの場合の動力数[-]
参考資料:新型軸流撹拌翼HR320とHR320Sの性能評価(化学工学論文集 2023 年 49 巻 3 号 p. 56-61)
撹拌翼表面粗さの影響
近年、3Dプリンターで撹拌翼を製作し性能評価する事例が増えています。
3Dプリンターは積層しながら製作する特性上、翼表面が粗くなります。
金属といえど撹拌装置は長期間の運用で欠けたり擦れたりと表面特性が変化します。
こうした運用や製法による変化を反映するため、撹拌翼表面粗さの所要動力におよぼす影響を評価する研究が行われました。
乱流域において、撹拌翼の表面粗さεと翼径dの比ε/ d≤0.0125では撹拌所要動力に影響を及ぼさないと報告されています。
参考資料
・最新ミキシング技術の基礎と応用
撹拌に関する詳細な計算方法が解説されています。
撹拌機の機械的強度の計算など、撹拌装置を設計するためのノウハウが詰め込まれておりオススメです。
-

-
最新ミキシング技術の基礎と応用(化学工学の進歩42)
www.amazon.co.jp
・プロセスケミストのための化学工学
化学プロセスの各要素に対する設計方法や注意点が解説されています。
実用的なプロセス設計を勉強したいときにオススメの書籍です。
-

-
プロセスケミストのための化学工学(基礎編)
www.amazon.co.jp
・化学工学ー解説と演習ー
化学工学を勉強したい!と思ったら真っ先にオススメしたい書籍です。
他の汎用化学工学書籍には無い「撹拌動力計算」や「撹拌伝熱計算」も記載されています。
-

-
化学工学―解説と演習ー
www.amazon.co.jp




