深さ1mの容器に水が満液にしてある。容器の側面の深さ90 cmのところに、【 ア 】直径20 mmの孔と【 イ 】直径10 mmの孔があいている。また、深さ45 cmのところに、【 ウ 】直径20 mmの孔と【 エ 】直径10 mmの孔があいている。次のA~Dの記述のうち、誤っているものの組合せはどれか。
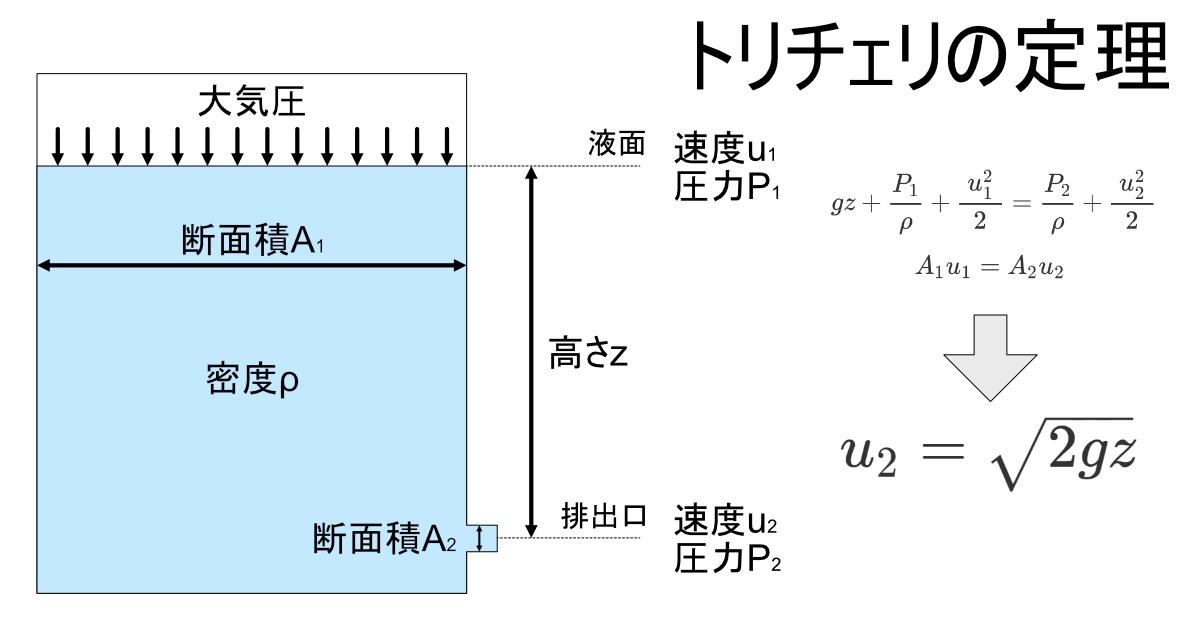
ただし、孔からの流速はトリチェリーの定理 \( u=\sqrt{2gh}\) が成り立つとする。uは流速、hは液深さ、gは重力の加速度である。
- 【 ア 】と【 イ 】では、ほぼ同じ流速である。
- 【 イ 】と【 ウ 】では、ほぼ同じ流量である。
- レイノルズ数が最も大きいのは、【 ア 】である。
- エタノールで満液にすると、どの孔でも水のときよりも流速が遅くなる。
選択肢
- A、C
- B、D
- A、D
- B、C
- C、D
解答解説
正答は2番です。
トリチェリの定理より、液面深さが同じである【 ア 】と【 イ 】では、ほぼ同じ流速です(A)。
【 ウ 】よりも【 イ 】の方が液面深さは2倍であるため、流速は【 イ 】の方が2倍となります。ノズル直径は【 イ 】が直径10 mm、【 ウ 】が直径20 mmと【 ウ 】が2倍大きいため、断面積は【 ウ 】が4倍大きくなります。流量は流速×ノズル断面積で計算できるため、【 ウ 】の方が【 イ 】よりも2倍の流量となります(B)。
| ノズル | ノズル高さ | 流速 | ノズル直径 | ノズル断面積 | 流量 |
|---|---|---|---|---|---|
| 【 ア 】 | 2H | 2u | 2D | 4A | 8uA |
| 【 イ 】 | 2H | 2u | D | A | 2uA |
| 【 ウ 】 | H | u | 2D | 4A | 4uA |
| 【 エ 】 | H | u | D | A | uA |
レイノルズ数はノズル径、流速、密度、粘度で変化します。同じ水を使用しているため密度と粘度は固定となります。流速とノズル径が共に一番大きい【 ア 】のレイノルズ数が一番大きくなります(C)。
レイノルズ数$$\frac{D u \rho}{\mu} $$D:配管内径[m]、u:流速[m/s]、ρ:密度[kg/m3]、μ:粘度[Pa・s]
本問いにおいては孔からの流速はトリチェリーの定理に従うため、液深さに依存します。エタノールに変更したとしても液深さが変わらないため流速は変化しません(D)。