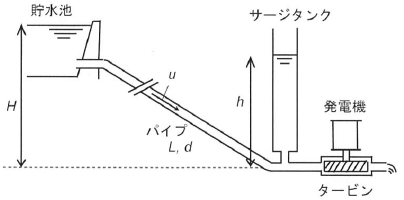
貯水池から長さL=1,000 m、管内径d=1.0 mのパイプを通して水を流し、水力発電機へ供給している。系の圧力変動を吸収するため下図のようにサージタンクが設けられている。基準高さからの貯水池水面高さはH=50 mである。サージタンク水面はh[m]の高さにあった。パイプ内の平均流速u=3.0 ms-1のとき、hとして、次のうち、最も近い値はどれか。ただし水の密度ρ=1,000 kg m-3、管摩擦係数f=0.0032、重力加速度g=9.8 m s-2。管内流れの圧力損失はΔP=-2fLu2ρ/d[Pa=kg m-1 s-2]である。
- 5 m
- 25 m
- 35 m
- 45 m
- 50 m
解答解説
正答は4番です。
まず貯水池の水からかかる位置エネルギーを求めます。ρgh(ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m])で[Pa]単位の位置エネルギーが計算できます。位置エネルギーは1000×9.8×50=4.9×105 Paとなります。
(単位変換参考)
ρgh:kg/m3×m/s2×m=kg / (m・s2)
Pa=N/m2= (kg×m/s2) / m2=kg / (m・s2)
配管内を流体が流れる時、摩擦によるエネルギー損失が発生します。その時のエネルギー損失量を圧力で表した圧力損失を計算します。計算式は問題に記載されているΔP=-2fLu2ρ/d[Pa=kg m-1 s-2]を用います。圧力損失は2×0.0032×1,000×3.02×1,000/1.0=5.76×104 Pa(0.576×105 Pa)となります。
サージタンクに液が流れ着いたとき、圧力損失により減少した4.9×105-0.576×105=4.324×105 Paのエネルギーが発生しています。この時のエネルギーを位置エネルギーの式から高さに換算すると、4.324×105 Pa÷1,000 kg m-3÷9.8 m/s2=44.12 mです。よって最も近い値は45 mです。



