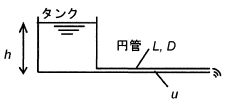
大気開放タンクに一定深さh=0.34 mで水が入っている。タンク底に長さL=1 m、管内径D=3 mmの円管を水平に接続し、大気中に水を流出させたとき、管内の平均流速u[m/s]として最も近い値はどれか?管入口出口間の圧力損失は、ΔP=4f (ρu2/2)(L/D)で計算され、これがタンク底の静水圧に等しい。ただし、管摩擦係数f=0.005、水の密度ρ=1,000 kg/m3、重力加速度g=9.8 m2/sとする。
- 0.1 m/s
- 0.3 m/s
- 1.0 m/s
- 3.0 m/s
- 20 m/s
解答解説
正答は3番です。
ベルヌーイの定理より、理想流体では位置エネルギーや圧力エネルギー、速度エネルギーの和が一定になることを利用します。つまりタンク液面部とタンク底部のエネルギ-は一定であると考えられます。
ベルヌーイの定理(圧力換算)[Pa]$$\rho gz+P+\frac{ \rho \ u^2\ }{2}=一定$$ρ:密度[kg/m3]、g:重力加速度[m/s2]、z:高さ[m]
P:圧力[Pa]、u:速度[m/s]
大気開放タンクのため圧力エネルギーは両位置においても大気圧がかかっており一定です。タンク液面部においてはタンク径が十分に大きく、タンク底から液が出る時に液面高さが変わらないとすると、速度エネルギーはゼロとみなせます。タンク底部においては高さがゼロであるため位置エネルギーがゼロとなります。よって理想流体においては、タンク液面の位置エネルギー(ρgh)はタンク底部の速度エネルギー(ρu2/2)に全て変換されます。更にここから流れによる損失を加味して計算します。
配管内を流体が流れる時、摩擦によるエネルギー損失が発生します。その時のエネルギー損失量を圧力で表した値が圧力損失です。問題では静水圧(タンク液面の位置エネルギー)と圧力損失が等しくなるとあります。圧力損失は問題に記載されているΔP=4f (ρu2/2)(L/D)を用います。
ρgh=4f (ρu2/2)(L/D)
gh=4f (u2/2)(L/D)
9.8×0.34=4×0.005×(u2/2)×(1/0.003)
上記方程式を解くと、管内の平均流速uは1.0 m/sです。



_問35.png)
