機械学習における線形代数の役割
まず線形代数の意味や機械学習における役割を解説します。
線形代数とは?
線形代数はベクトルや行列のような数の並びを用いて数学的な問題を解くための学問です。
例えば、複数の変数を含む方程式を解く、複数の方程式を同時に解く、グラフを変形するなどの問題を解決するために使われます。
機械学習では、行列やベクトルを使って効率的に大量のデータを処理するための役割があります。
数式を読みやすくできる
機械学習では線形代数を使って数式を簡素に表現しています。
つまり、式を理解するために線形代数の知識が必須です。
例えば、一般に重回帰分析の式は以下のように表されます。
重回帰分析の式
$$ \begin{align}y & =w_{1}x_{1}+w_{2}x_{2}+\cdots+w_{n}x_{n}+b\\\\
& =\sum_{i=1}^nw_{i}x_{i}+b \end{align}$$
この式は線形代数(ベクトル)を使うと非常に簡単に表現できます。
線形代数で重回帰分析を表現
$$ y=\boldsymbol{w^\mathrm{T}x} +b$$
線形代数を使うことで表現が簡単になる一方で抽象化しますので、式を見て具体的にイメージ出来るようになることが重要です。
スカラー・ベクトル・行列
線形代数を学ぶにあたりスカラー・ベクトル・行列の定義を理解しなければなりません。
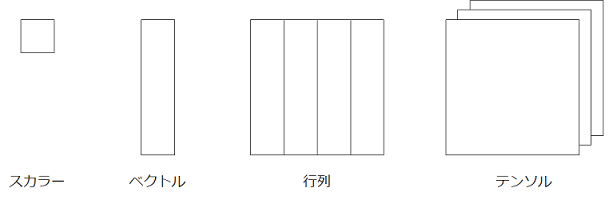
スカラー
スカラーは3や10、582、x、yなど、1つの値や変数を指します。
スカラーの例
$$ 3、10、582、x、y$$
ベクトル
ベクトルはスカラーを1方向に並べた集合体です。
数式では、よく小文字かつ太字表記されます。
ベクトルの例
$$ \boldsymbol{x}_3=\left(\begin{array}{c}x_1 \\ x_2 \\ x_3\end{array}\right)
\boldsymbol{x}_n=\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right)$$
先に紹介した重回帰分析は、このベクトルを使って表現されています。
ベクトルは縦向きと横向きで意味が変わります。
機械学習においては、一般に縦ベクトルを基準として考えられています。
もし表記上、縦ベクトルを横向きに書きたい場合はカンマで区切って記載することもあります。
カンマを使った縦ベクトルの例
$$ \boldsymbol{x}_3=\left(x_1,x_2,x_3\right)$$
縦ベクトルを横ベクトルとして扱いたい場合には後ほど解説する転置という記号をつけて表現します。
行列
行列は同じサイズのベクトルを複数個並べた集合体です。
数式では、よく大文字かつ太字表記されます。
行列の例
$$ \boldsymbol{A}=\begin{bmatrix}6 & 2 \\1 &1 \\9 & 4 \end{bmatrix} \boldsymbol{X}=\begin{bmatrix}x_{11} & x_{12} \\x_{21} & x_{22} \end{bmatrix}$$
行列の縦方向を行、横方向を列と呼びます。
左上を1行1列目の値として下方向が2行目・3行目……で、右方向が2列目・3列目……です。
上式ではAが3行2列、Xが2行2列、もしくは3×2や2×2の行列と表現します。
テンソル
メインはスカラー・ベクトル・行列ですが、テンソルも紹介します。
テンソルは行列を深さ方向に複数枚重ねた集合体です。
例えば画像データではテンソルが使われます。
画像データは0~255画素のスカラー(ピクセル)を集めた行列での表現が基本で、更にRGBの3色に重ねたテンソルとして扱います。
基本的な演算
ここからはベクトルや行列を使った基本的な演算について解説します。
足し算・引き算
ベクトルや行列の足し算や引き算は同じ要素同士を足します。
ただしサイズが同じでなければ演算できません。
ベクトルの足し算と引き算
$$ \begin{align}\left(\begin{array}{c}1\\ 5\end{array}\right)+\left(\begin{array}{c}6\\ 3\end{array}\right)
&=\left(\begin{array}{c}{1+6}\\ {5+3}\end{array}\right)
=\left(\begin{array}{c}7\\ 8\end{array}\right)\\\\
\left(\begin{array}{c}1\\ 5\end{array}\right)-\left(\begin{array}{c}6\\ 3\end{array}\right)
&=\left(\begin{array}{c}{1-6}\\ {5-3}\end{array}\right)
=\left(\begin{array}{c}-5\\ 2\end{array}\right)\end{align}$$
行列も同様です。
行列の足し算と引き算
$$ \begin{align}
\begin{bmatrix}7 & 3 \\1 & 9 \end{bmatrix}+\begin{bmatrix}5 & 1 \\6 & 4 \end{bmatrix}
&=\begin{bmatrix}7+5 & 3+1 \\1+6 & 9+4 \end{bmatrix}
=\begin{bmatrix}12 & 4 \\7 & 13 \end{bmatrix}\\\\
\begin{bmatrix}7 & 3 \\1 & 9 \end{bmatrix}-\begin{bmatrix}5 & 1 \\6 & 4 \end{bmatrix}
&=\begin{bmatrix}7-5 & 3-1 \\1-6 & 9-4 \end{bmatrix}
=\begin{bmatrix}2 & 2 \\-5 & 5 \end{bmatrix}
\end{align}$$
スカラー倍
ベクトルや行列にスカラーをかけることで各要素をスカラー倍できます。
ベクトルや行列のスカラー倍
$$ \begin{align}
10\left(\begin{array}{c}2\\ 6\end{array}\right)
&=\left(\begin{array}{c}20\\ 60\end{array}\right)\\\\
10\begin{bmatrix}2 & 8 \\6 & 5 \end{bmatrix}
&=\begin{bmatrix}20 & 80 \\60 & 50 \end{bmatrix}
\end{align}$$
内積
ベクトルや行列同士を掛け算する時は少し特殊な形です。
基本の形は横ベクトル(行ベクトル)と縦ベクトル(列ベクトル)のかけ算です。
ベクトルの内積
$$ \begin{align}
\boldsymbol{w}^\mathrm{T}\boldsymbol{x}
&=\left(\begin{array}{c}w_1 \ w_2 \ \cdots \ w_n\end{array}\right)\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right)\\\\
&=w_{1}x_{1}+w_{2}x_{2}+\cdots+w_{n}x_{n}
\end{align}$$
このような演算を内積と呼びます。
内積は重回帰分析やディープラーニングの基礎となる計算です。
行列においてもベクトルと同様の計算方法です。
行列の内積
$$ \begin{align}
\boldsymbol{AB}
&=\begin{bmatrix}a_{1} & a_{2} \\a_{3} & a_{4} \end{bmatrix}
\begin{bmatrix}b_{1} & b_{2} \\b_{3} & b_{4} \end{bmatrix}\\\\
&=\begin{bmatrix}
a_{1}\times b_{1}+a_{2}\times b_{3} & a_{1}\times b_{2}+a_{2}\times b_{4}
\\a_{3}\times b_{1}+a_{4}\times b_{3} & a_{3}\times b_{2}+a_{4}\times b_{4}
\end{bmatrix}
\end{align}$$
行列の内積を計算できるための条件があります。
それはa行b列×c行d列の場合、bとcが同じ数値であることです。
また行列”A×B”と”B×A”は結果が異なりますので注意してください。
転置
ベクトルや行列の向きを変えることを転置と呼びます。
記号の右上にTをつけて表現します。
行列においては例えば2行3列の行列を3行2列に転置します。
ベクトルや行列の転置
$$ \boldsymbol{A}=\begin{bmatrix}a_{11} & a_{12} \\ a_{21} & a_{22} \\a_{31} & a_{32} \end{bmatrix} \Leftrightarrow
\boldsymbol{A}^\mathrm{T}=\begin{bmatrix}a_{11} & a_{21}& a_{31} \\ a_{12} & a_{22}& a_{32} \end{bmatrix}$$
行列同士が掛け合わされた要素が転置されている場合、以下のように変換可能です。
転置の特徴
$$ \begin{align}
\left(\boldsymbol{AB}\right)^\mathrm{T}&=\boldsymbol{B}^\mathrm{T}\boldsymbol{A}^\mathrm{T}\\\\
\left(\boldsymbol{ABC}\right)^\mathrm{T}&=\boldsymbol{C}^\mathrm{T}\boldsymbol{B}^\mathrm{T}\boldsymbol{A}^\mathrm{T}
\end{align}$$
特別な行列
行列にはある特徴を持つ名前が付けられた行列が存在します。
正方行列
行と列の数が等しい行列を正方行列と呼びます。
単位行列
左上から右下に向かっての方向(対角方向)の値が1、その他を0としたときの行列を単位行列と呼びます。
一般的にはIやEで表記されます。
対角を1であるため、単位行列は正方行列です。
単位行列の例
$$ \begin{bmatrix}1 & 0 \\0 & 1 \end{bmatrix} \begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1 \end{bmatrix}$$
ある行列に単位行列をかけても変化しません。
役割が数字の1と同じであることから単位行列と呼ばれています。
逆行列
行列にある行列をかけると単位行列になるものを逆行列と呼びます。
一般的には元の行列に対して-1乗で表記されます。
2×2行列の逆行列
$$ A=\begin{bmatrix}a & b \\c & d \end{bmatrix} \Leftrightarrow A^{-1}=\begin{bmatrix}d & -b \\-c & a \end{bmatrix}$$
役割が数字の逆数と同じであることから逆行列と呼ばれています。
逆行列が存在するためには以下の条件が必要で、その条件を満たす行列は正則行列と呼ばれます。
- 正方行列であること
- 行列式が0でないこと
計算量の関係から2×2、3×3のサイズの行列までは逆行列が何とか手計算できますが、それ以上は計算ツールやプログラミングにより計算するのが一般的です。
行列式はdetAや|A|のように表現します。
2×2行列の行列式
$$ A=\begin{bmatrix}a & b \\c & d \end{bmatrix} \Leftrightarrow det\boldsymbol{A}=\begin{vmatrix}\boldsymbol{A}\end{vmatrix}=ad-bc$$
オススメ書籍
・多変量解析法入門
重回帰分析や主成分分析、クラスター分析などデータ分析の基本となる要素を順を追って分かりやすく解説してくれます。
20年以上経った今でも多くの方にオススメされる書籍です。
-

-
多変量解析法入門
www.amazon.co.jp
・データ分析に必須の知識・考え方 統計学入門
データ分析することに目線を置いた統計学の入門書です。
学問を体系的に学ぶことより実務面に寄った学習をしたい方にオススメです。
-

-
データ分析に必須の知識・考え方 統計学入門
www.amazon.co.jp
・化学、化学工学のための実践データサイエンス
化学プロセスで得られるデータの前処理や変数選択、可視化、機械学習と1冊で体系的に学べる書籍です。
少しデータ分析を実施したことがある中級者向けの書籍ですが、化学はじめプロセス製造に携わる方なら是非とも読んでおきたい書籍です。
-

-
化学・化学工学のための実践データサイエンス ―Pythonによるデータ解析・機械学習
www.amazon.co.jp


