口径(内径)3.0 mmのノズルから噴水が20 mの高さに上がっている。
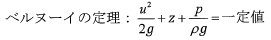
u:流速[m/s]
g:重力加速度 9.8m/s2
z:位置[m]
p:圧力[Pa]
ρ:流体密度[kg/m3]
を用いると、水の単位時間当たりの噴出量[L / 分]の最も近い値はどれか。

- 504
- 165
- 10.7
- 8.4
- 5.9
解答解説
正答は4番です。
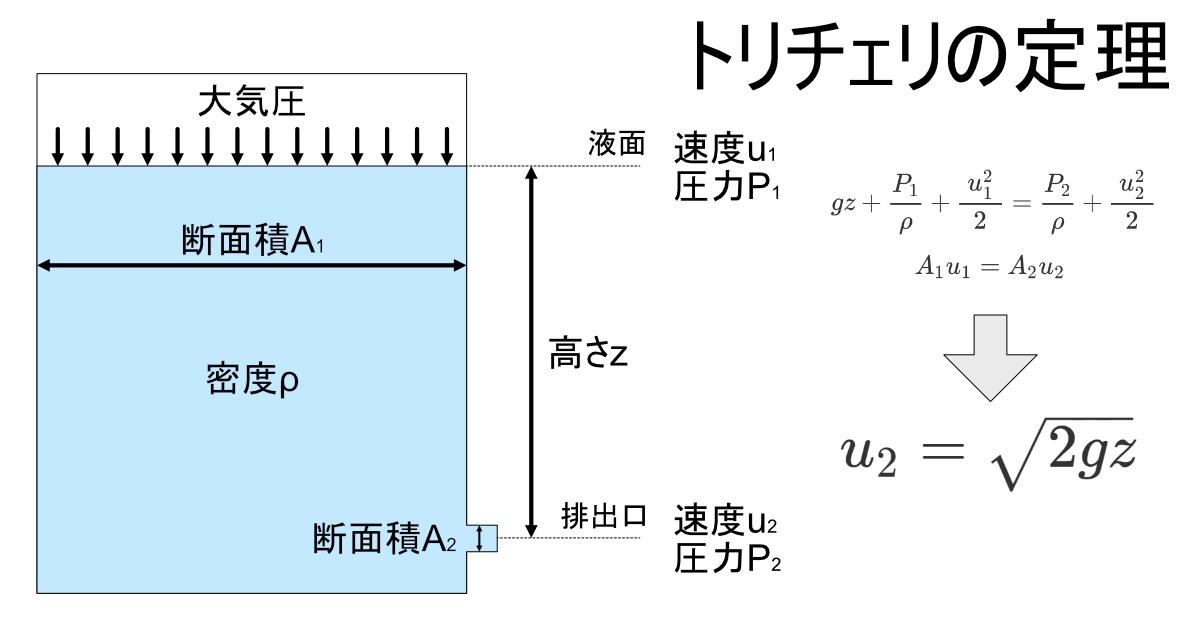
まず、ベルヌーイの定理を用いて噴出速度を求めます。ノズルの出口と噴水の最高点で適用すると、両点で大気圧がかかる事は同じなため圧力項p/ρgは無視できます。またノズル出口のポテンシャル(位置)項zは0、ノズル噴水最高点の速度項u2/2gは0です。u2/2×9.8=20と立てられ、u=20 m/sです。この考え方により導かれる速度式はトリチェリの定理と呼ばれます。
ノズルの断面積は(0.003)2π/4 m2であり、流量Qは20 m/s × (0.003)2π/4 m2=1.41 × 10-4 m3/sです。回答の単位L/minに合わせると、1.41 × 10-4 m3/s × 60 × 1000=8.49 L/minとなり、最も近い値は8.4 L/minです。