ゴム製水風船に炎をあてても、短時間では風船は破れない。この現象を「気相(燃焼ガス)境膜-ゴム製の壁-液相(水)境膜」とした、「固体壁を通しての2流体間の対流伝熱」のモデルで解け。その結果、風船外側表面温度T1として最も近い値はどれか。ただし、水の温度T3=20℃、水側の伝熱係数h3=1000 W/(m2 K)、風船ゴムの厚さδ=200 μm、風船ゴムの熱伝導率λ=0.13 W/(m K)、燃焼ガス温度T0=800℃、燃焼ガス側の伝熱係数h0=5.0 W/(m2 K)とする。
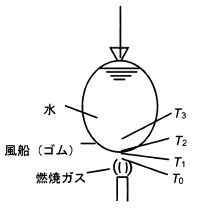
- 41℃
- 30℃
- 25℃
- 24℃
- 20℃
解答解説
正答は2番です。
固体の熱流束はフーリエの法則q=-k(dT/dx)から計算できます。(dT/dx)は温度の変化量dTと距離の変化量dxの比であることを表します。
熱流束qの単位Wm-2はWを変形してJ/s・m-2とも記載できます。つまり熱流束は、ある断面に対して直交する方向に伝わる、単位時間当たりの熱量を意味します。そのため皮膚と空気のように密着して連続的に伝熱する状態では、同一面積におけるゴムと水と空気の伝熱量(熱流束)が同じとして計算できます。
フーリエの法則より、ゴムの熱流束は0.13 W/(m K) × (T1-T2) K / 0.0002 m=650T1-650T2 W/m2です。
空気の熱流束は5.0 W/(m2 K) × (800-T1) K=4,000-5T1 W/m2です。
水の熱流束は1,000 W/(m2 K) × (T2-20) K=1,000T2-20,000 W/m2です。
今回はT1およびT2が不明な値です。この場合、総括伝熱係数から一連の熱流束計算したうえでそれぞれの温度を求めます。
1/U=1/5+0.0002/0.13+1/1,000
U=4.9375 W/(m2 K)
熱流束は4.9375×(800-20)=3851.25 W/m2です。空気の熱流束の式を用いて、4,000-5T1=3851.25となり、T1=29.8℃です。よって、最も近い値は30℃です。同様に計算するとT2=23.9℃です。



