平成28年度 問35

　1辺4 mの四角形の水槽がある。水槽には底面から高さ100 mmの所に内径φ20 mmのノズルが付いている。この水槽に水を入れ、そのノズルより排出される水の量を計測したところ10秒間に0.013 m³であった。このときの水槽の液深として次のうち、最も近い値はどれか。
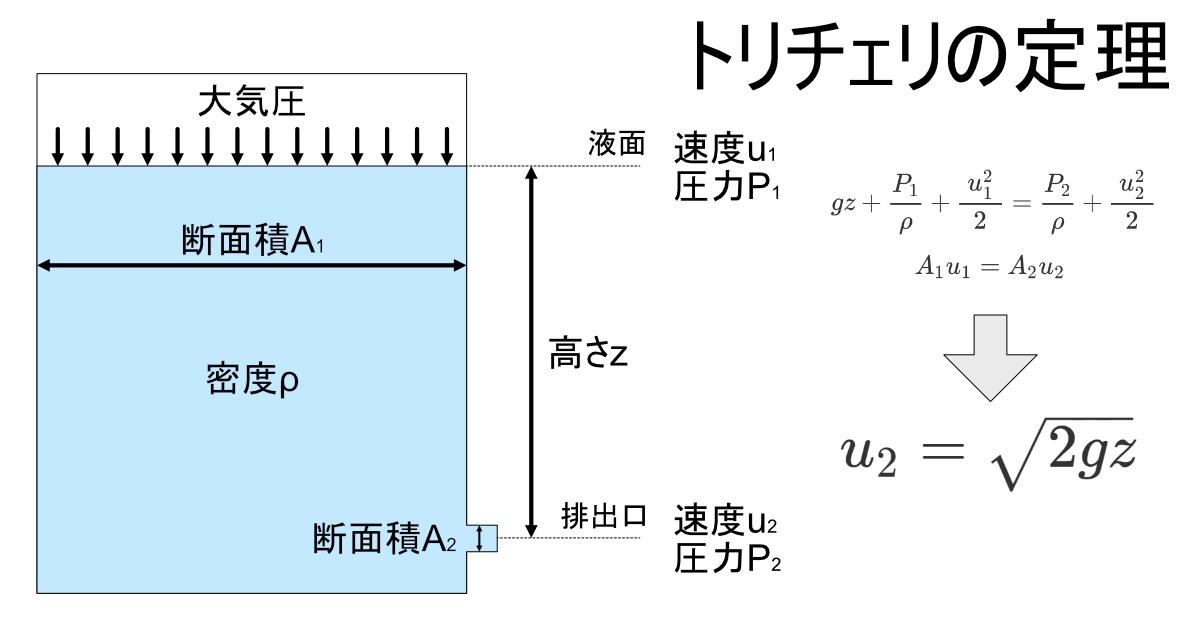
　なお、ノズルから水が流出するときの圧力損失は考慮しないものとし、ノズルからの水の流出速度はトリチェリの定理u＝（2gH）^1/2に従うものとする。
u：流出速度（単位面積単位時間当たりの排出量）［m s^-1］
H：ノズル位置からの水面の高さ［m］
g：重力加速度9.8 m s^-2
水の密度：1,000 kg m^-3

1. 0.57 m
2. 0.67 m
3. 0.77 m
4. 0.87 m
5. 0.97 m

解答解説

正答は5番です。

内径φ20 mmのノズルであるため、断面積は0.02²π/4＝0.000314 m²です。

そのノズルから排出される水が10秒間に0.013 m³であるため、流量は0.013 m³/10＝0.0013m³/sです。

流量と断面積より、ノズルからの水の流出速度uは（0.0013m³/s）/（0.000314 m²）＝4.14 m/sとなります。

トリチェリの定理u＝（2gH）^1/2を用いてノズル位置からの水面の高さを求めると4.14＝（2×9.8×H）^1/2となり、H＝0.87 mmです。

（式変形参考）
4.14＝(2×9.8×H)^1/2
(4.14)²＝{(2×9.8×H)^1/2}²
(4.14)²＝(2×9.8×H)
H＝(4.14)²/(2×9.8)
H＝0.87

ノズルは底面から高さ100 mmの所に取り付いているため、水槽の液深は0.874＋0.1＝0.97 mmです。

参考資料

「トリチェリの定理」の考え方

トリチェリの定理はベルヌーイの定理から導かれる代表的な近似式です。 タンク出口から液が排出されてもタンク液面高さが極微小しか変化しない時、トリチェリの定理が適用できます。 ベルヌーイの定理から導出して ...