平成23年度 問30

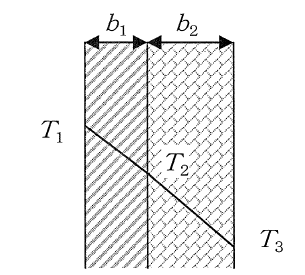
2種類の材料から構成される炉壁がある。内側は厚さb₁=10 mmの耐火レンガで熱伝導率はk₁=0.90 W・m^-1・K^-1、外側は厚さb₂=20mmの断熱レンガで熱伝導率はk₂=0.12 W・m^-1・K^-1である。炉壁の内外表面温度がそれぞれT₁=1,200 K, T₃=350 Kの場合、レンガの接触面温度T₂に最も近いものは次のうちどれか。

1. 403 K
2. 917 K
3. 1,100 K
4. 1,150 K
5. 1,180 K

解答解説

正答は4番です。

この問題はフーリエの法則q＝－k（dT/dx）を用いて計算します。（dT/dx）は温度の変化量dTと距離の変化量dxの比であることを表します。つまり今回は温度減少量と伝熱距離の比に相当します。

• 耐火レンガの熱流束q₁：-0.90×（1,200－T₂）/ 0.010
• 断熱レンガの熱流束q₂：-0.12×（T₂-350）/ 0.020

熱流束qの単位Wm^-2はWを変形してJ/(s・m²)とも記載できます。つまり熱流束は、ある断面に対して直交する方向に伝わる、単位時間当たりの熱量を意味します。そのため断熱材1と2のように密着して連続的に伝熱する状態では、各断熱材における熱流束q₁とq₂の値は同じとなります。

各断熱材における熱流束を求めた2式で方程式を解くとT₂＝1,146.9℃と求まります。よって最も近いものは1,150℃です。

参考資料

【熱交換器】伝熱計算の基礎知識

2流体の流れ方向 熱交換器の高温側流体と低温側流体の流れ方向によって伝熱結果が大きく異なります。 並流 両流体が同じ方向に流れる並流では、低温側の温度が高温側の温度を超えないのが特徴です。 これは入口 ...