令和2年度 問32

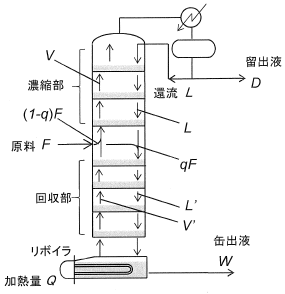
下図に段型連続蒸留塔内部の気液流れ等を示す。F：原料、D：留出液、W：缶出液、V：濃縮部蒸気流量、L：濃縮部蒸気流量、L’：回収部液流量、V’：回収部蒸気流量で、これら流量は［mol・s^-1］単位である。q［-］は供給原料の液割合である。Q［W］はリボイラの加熱量であり、回収部蒸気流量V'はQに比例する。F＝1mol・s^-1、q＝0.5、D＝0.3mol・s^-1の条件で操作するとき、還流比R＝2から還流比R＝6に変えるために、Qは何倍にするべきか、次のうち最も適切なものはどれか。

1. 2倍
2. 2.5倍
3. 3倍
4. 4倍
5. 5倍

解答解説

正答は4番です。