平成29年度 問35

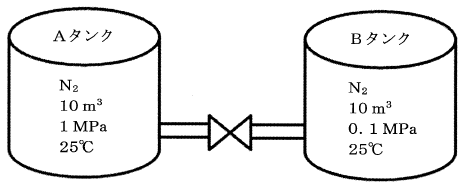
　バルブを介して遮断されている2基の密閉したタンクがある。Aに示した10 m³のタンクには1 MPaの窒素ガスが充填されており、Bタンクの容量も10 m³であり、0.1 MPaの窒素ガスが充填されている。温度はともに25℃である。遮断しているバルブを時間をかけて開け、2基のタンク内の圧力が均一で平衡となったときのBタンクの温度に最も近い値はどれか。
　ただし、窒素ガスは理想気体とし、外部からの入熱は無視する。また、定圧比熱Cp、定容比熱Cvとして、Cp/Cv=1.4とする。

1. -47℃
2. 19℃
3. 25℃
4. 33℃
5. 47℃

解答解説

正答は3番です。

理想気体の内部エネルギーは温度にのみ依存し、U=nCvTで表されます。n はモル数、Cvは定容比熱、Tは温度です。

それぞれの内部エネルギーはU_A​＝n_A​Cv​T_A​、U_B＝n_B​Cv​T_Bです。また混合後の全内部エネルギーはU_total​＝(n_A＋n_B​)​Cv​T_finalです。

​断熱過程で外部との熱の出入りがないので、エネルギー保存則からU_total​＝U_A＋​U_Bとなります。

よって代入すると、(n_A＋n_B​)​Cv​T_final＝n_A​Cv​T_A＋n_B​Cv​T_Bです。両タンクの温度は同じであることからT＝T_A＝T_Bとして計算します。

(n_A＋n_B​)​Cv​T_final＝n_A​Cv​T_A＋n_B​Cv​T_B
(n_A＋n_B​)​Cv​T_final＝n_A​Cv​T＋n_B​Cv​T
(n_A＋n_B​)​​T_final＝n_A​T＋n_B​​T
(n_A＋n_B​)​​T_final＝(n_A＋n_B)​​T
T_final＝T

よって、バルブを開けた後の温度はT_final＝T＝25℃です。

問題に定圧比熱Cp、定容比熱Cvとありますが、液体の場合は体積変化が少ないためCp/Cv≒1.0です。気体の場合、定圧比熱Cpにおいては温度上昇のみならず膨張による外部への仕事の分だけ定容比熱Cvよりも大きくなります。