平成27年度 問32

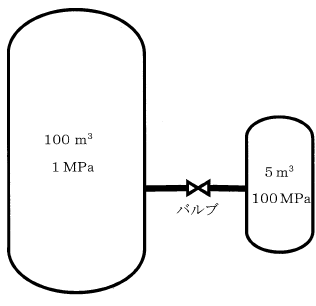
　バルブを介して遮断されている2基の密閉したタンクがある。100 m³のタンクには1 MPaの気体が充填されており、5 m³のタンクには100 MPaの気体が充填されている。気体は共に同じもので理想気体であり。温度は共に25℃である。遮断しているバルブを開けて、2基のタンク内の圧力を均一とした場合の圧力として、最も適切な値はどれか。
　なお、断熱膨張は考慮せず。温度は25℃一定とする。
　また、気体の状態方程式はPV=nRTであり、Pは圧力［MPa］、Vは容積［m³］、nは気体のmol数［mol］、Rは気体定数［MPam³mol^-1K^-1］、Tは気体の温度［K］である。

1. 5.3 MPa
2. 5.5 MPa
3. 5.7 MPa
4. 5.9 MPa
5. 6.1 MPa

解答解説

正答は3番です。