平成24年度 問35

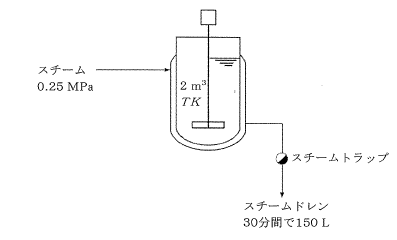
　下図のように、2 m³のジャケット付撹拌槽に水温T Kの水を2 m³仕込み、0.25 MPaの飽和スチームで加熱した。ジャケットから排出されたスチームドレンは30分間で、150 Lであった。このとき、槽内の水温の上昇分として、最も近い値はどれか。
　ただし、水の比熱は4,187 J kg^-1 K^-1、水の密度は1,000 kg m^-3とする。また、圧力に対するH_L（飽和水の比エンタルピー）、及びH_g（飽和スチームの比エンタルピー）は下表のとおりとする。なお、槽の昇温、放熱、トラップ等での熱損失は考慮しないものとする。

1. 38.4 K
2. 39.1 K
3. 39.8 K
4. 40.5 K
5. 41.2 K

解答解説

正答は2番です。