高分子の固有粘度[η]は、希薄溶液の濃度依存性の測定値から、次式を用いて求めることができる。
$$ \left[\eta\right]=\lim_{c\rightarrow 0}\left(\eta/\eta_{s}-1\right)/c$$
ここで、c:濃度(g/cm3)、η:高分子溶液の粘度、ηs:溶媒の粘度
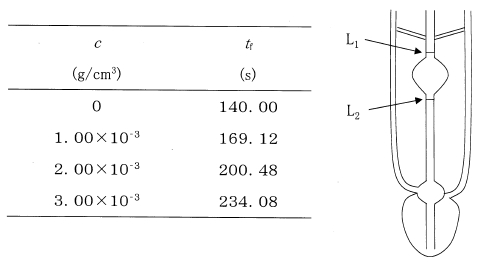
古典的には図のような毛細管粘度計を用いて、異なる濃度cでの高分子溶液の表面が点L1からL2までに落ちる流下時間tfをそれぞれ測定することによって求めることができる。この際、tfは溶液粘度ηに比例することになる。ある高分子希薄溶液について、この粘度測定を行い、下のような結果が得られた場合、固有粘度として最も近い値はどれか。
- 100 cm3/g
- 200 cm3/g
- 230 cm3/g
- 270 cm3/g
- 1500 cm3/g
解答解説
正答は2番です。
高分子を溶媒に溶かすと、分子量の大きい高分子を用いるほど溶液の粘度が高くなります。一般にポリマーの分子量に依存するため、この特性を生かし、固有粘度(極限粘度)から分子量を計算できます。これをMark-Houwink-Sakuradaの式と呼びます。
Mark-Houwink-Sakuradaの式
$$ \left[ \eta \right] = KM^{\alpha}$$
[η]:固有粘度、M:分子量、K, α:高分子と溶媒で決まる定数
ポリマーの分子量を計算するために問題の方法(粘度法)を用いて固有粘度を調べます。測定結果を横軸にc、縦軸に(η/ηs−1)/c の形でプロットし、直線がc=0の時の(η/ηs−1)/c の値が固有粘度[η]です。
ポリマーが溶解されていないとき(c=0のとき)、高分子溶液の粘度ηは溶媒の粘度ηsと一致します。そのため2つの粘度の比率η/ηsは1となります。
問題文中に流下時間tfは溶液粘度ηに比例すると記載されています。また溶媒は1種類で一定なため、ポリマーが増加したことによるη/ηsの変化率はtfの変化率と一致します。これら内容を踏まえ、縦軸の値となる(η/ηs−1)/c を求めます。
| 濃度 c [g/cm3] | 流下時間 tf[s] | 粘度の比率 η/ηs[-] | (η/ηs−1)/c[cm3/g] |
|---|---|---|---|
| 0 | 140.00 | 1 | ゼロ割りのため計算不可 |
| 1.00×10-3 | 169.12 | 1.208 | 208 |
| 2.00×10-3 | 200.48 | 1.432 | 216 |
| 3.00×10-3 | 234.08 | 1.672 | 224 |
横軸にc、縦軸に(η/ηs−1)/c でプロットしたグラフを以下に示します。
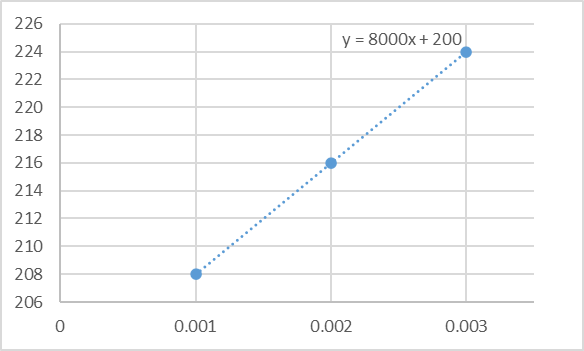
近似直線はy=8000x+200です。x=0、つまり濃度c=0のときの(η/ηs−1)/cが固有粘度[η]であるため、値は200となります。
参考資料
-
-
極限粘度
www.ube.co.jp
-
-
高分子の分子量
main.spsj.or.jp


