令和3年度 問34

　排水中に直径d_p＝6.0×10^-5 m、粒子密度ρ_p＝1200 kg/m³の粒子のみが懸濁している。粒子の沈降速度u_t［m/s］は次式のストークスの式に従うものとする。
　　ストークスの式：u_t＝（ρ_p－ρ）gd_p² / 18μ
　ここで、ρ：水の密度（＝1000 kg/m³）、g：重力加速度（＝9.8 m/s²）、μ：水の粘度（＝0.0010 Pa s）である。
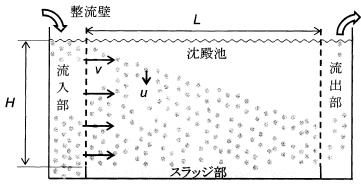
　深さH＝5 mの横流式沈殿池（下図）を用いてこのd_p、ρ_pの粒子のみを含む排水から粒子を60%除去したい。そのために必要な沈殿池の長さL［m］として、最も近い値はどれか。ただし、水の流れは水平方向の速度v＝0.0034 m/sで均一とする。

1. 17 m
2. 26 m
3. 43 m
4. 50 m
5. 59 m

解答解説

正答は2番です。

ストークスの式を解きます。

u_t＝（1,200－1,000）× 9.8 × (6 × 10^-5)² / (18 × 0.0010)
u_t＝200× 9.8 × 36 × 10^-10 / (18 × 10^-3)
u_t＝0.000392 m/s

粒子の60％を除去するため、高さ5 mの60％沈降すれば良い計算となります。沈降に要する時間は5 × 0.6 / 0.000392＝7653 sです。

水の水平方向の流れを考えると、必要となる距離は7653 × 0.0034＝26 mです。